728x90
반응형
도수 : 자료의 빈도수
상대도수 : 도수/전체도수
데이터의 시각화
: 자료를 분석해 한 눈에 볼 수 있도록 도표나 차트 등으로 정리하는 것
일변량 차트(Univariate Charts)
1. 범주형
2. 수치형
- 히스토그램 - 데이터의 중심을 알 수 있음. 그룹을 알 수 있음. 이상치의 유무를 알 수 있음
- 1개의 Box plot - Min부터 Q1, Q1부터 Q2, Q2부터 Q3, Q3 부터 Max 각 갯수는 같은데 분포가 다름. 대칭 비대칭 알 수 있음.
다변량 차트(Bivariate Charts)
1. 범주형 & 수치형 - Box plot/Bar chart
2. 수치형 & 수치형 - Scatter plot - X,Y 관계가 있는 것 알 수 있음 하지만 X,Y 의 의과관계는 알 수 없음
위치 통계량(중심 경향성)
1. 평균(산술 평균) - 주어진 수의 합을 수의 개수로 나눈 값(유일한 값, 극단적인 경우 대표값의 기능을 상실)
2. 중앙값(Median) - 분포의 한가운데 수
3. 최빈값(Mode) - 가장 자주 나타나는 수 (아에 존재 하지 않을 수도 있고, 여러 개 나올 수도 있음)

변이 통계량(퍼짐 정도)

표본인 경우,
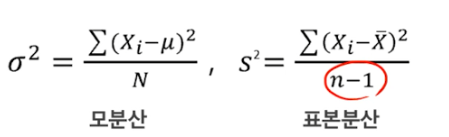
분산 및 표준편차 구할 때 N-1 로 나눠주어야 함 (불편 추정량 때문, 모수랑 비슷한 값을 만들어 주는 추정량)
변동계수(변이 계수)
: 표준 편차를 평균으로 나눈 값
표준 편차 - 평균에서 데이터들이 얼마나 떨어져 있나
But, 데이터 스케일이 다를 경우 표준편차만 갖고 구분하기에는 정확하지 않을 수 있다.
표준편차를 평균으로 나누면 실제로 평균 중심으로 얼마나 퍼져있는지 더 정확하게 알 수 있다.
728x90
반응형
'Data Science' 카테고리의 다른 글
| 상관분석 (0) | 2025.01.13 |
|---|---|
| 추정 (0) | 2025.01.12 |
| 주요확률분포 (0) | 2025.01.11 |
| 확률 & 베이즈 정리 (0) | 2025.01.09 |
| 기본 용어 (0) | 2025.01.09 |


