확률 변수 : 표본공간의 원소를 특정숫자인 실수로 대응한 값
확률 분포 : 확률변수와 그 값이 나올 수 있는 학률을 대응시켜 표시하는 것
이산확률분포
- 동전 3개를 던졌을 때 앞면이 나온 수의 확률 분포
| x ;확률변수 | 0 | 1 | 2 | 3 |
| p(X=x) ;확률분포 | 1/8 | 3/8 | 3/8 | 1/8 |
확률질량함수
- 이산형 확률변수에 대응되는 확률 분포
- f(x)=P(X=x), f(x)>=0
- 누적 분포 함수 F(x)는 0<=F(x)<=1

기대값(평균) E(X)=μ
1. E(a)=a
2. E(a+bX)=a+bE(X)
3. E(X+Y)=E(X)+E(Y) : 두 확률변수의 합의 기댓값은 각 확률변수의 기댓값의 합과 같음
4. E(aX+bY)=aE(X)+bE(Y)
5. E(X2)≠{E(X)}2
분산(편차 제곱의 평균) : 확률분포의 흩어진 정도를 측정
1.Var(a) = 0
2. Var(a+x) = Var(x)
3. Var(bx) = b2Var(x)
4.Var(x+y) = Var(x) + Var(y) : 독립일 경우
5.Var(x+y) = Var(x) + Var(y) + 2Cov(x,y)
균등분포(Uniform Distribution)


이항분포
:베르누이 실험 또는 베르누이 시행에 기초하고 있으며 베르누이 시행을 n번 반복하면 이항실험이 된다.


이항분포의 형태는 모수인 시행횟수 n과 성공확률 P의 값에 따라 결정된다.
성공확률 P=0.5에 가까우면 시행횟수 n의 크기에 관계없이 이항분포는 좌우대칭의 종모양을 이룬다.
시행횟수 n이 크면 성공확률 p의 크기에 관계없이 이항분포는 좌우대칭을 이룬다.
p<1/2 이고, n이 작은 경우에 이항분포는 오른쪽 꼬리분포를 나타낸다.
p>1/2 이고, n이 작은 경우에 이항분포는 왼쪽 꼬리분포를 나타낸다.
기대값(평균) E(x) = np
분산 = np(1-p)
포아송분포(Poisson Distribution)
:일정한 단위시간, 단위거리, 단위면접과 같이 어떤 구간에서 어떤 사건이 랜덤하게 발생하는 경우에 사용할 수 있는 이산형 확률분포
주로 ~동안 이 문제에 나옴.
사건 발생( λ)
기대값 E(x) = 분산 = λ
λ가 커질수록 정규분포를 따라간다.
★ 단위 시공간
지수분포(Exponential Distribution)
:사건이 서로 독립일 때, 일정 시간 동안 발생하는 사건의 횟수가 포아송 분포를 따른다면, 다음 사건이 일어날 때까지 대기시간이 지수분포특정 시간 당 발생횟수가 많아지면 많아질수록 대기 시간이 낮아짐

평균 = 1/ λ분산 = 1/ λ2
★ 대기 시간
정규분포(Normal Distribution)
:연속 확률 변수를 기술하는 가장 중요한 확률 분포
종같이 보이는 부드러운 곡선
중심극한정리에 의하여 독립적인 확률변수들의 평균은 정규 분표에 가까워지는 성질이 있기 때문에 수집된 자료의 분포를 근사하는 데에 자주 사용된다.
표본들의 평균을 평균낸 값은 정규분포를 따른다.
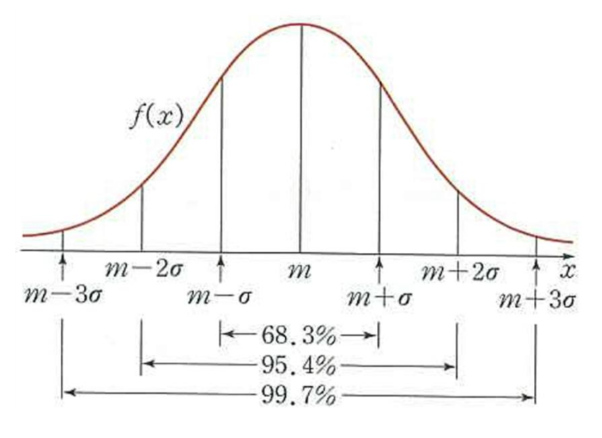
±2σ 사이에 95.4%의 데이터가 포함되어 있다.
★ 종 모양
표준정규분포
표준화를 통하여 서로 다른 평균과 분산을 가진 분포(어떤 형태든 Z분포로 바꾸면) 사이의 비교가 가능
확률변수 Z가 평균 = 0 , 분산 = 1 인 정규분포 , Z분포라고도 부른다.
-1.96 ~ 1.96 안 95% 데이터가 있다.
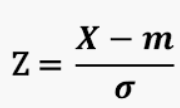
T분포(Student's t-Distribution)
:모집단의 평균을 추론하고 싶을 때 사용
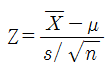
분모에 표준오차값, 여러 표본들로부터 얻은 표본통계량의 변량 (개별 데이터 값들의 변량을 뜻하는 표준편차와 혼동하지 말 것)
- 표준편차: 개별 데이터 포인트의 변동성을 측정하는 지표 (S)
- 표준오차: 표본 측정 지표의 변동성을 측정하는 지표(SE)
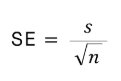
★ 모집단 평균 추론 시, 표본이 적은 경우 사용
카이제곱 분포(Chi-squared Distribution)
:표본을 가지고 모집단의 분산을 추론하고 싶을 때 사용
항상 양수이며, 심하게 왼쪽으로 쏠린 분포로 자유도에 따라 모양이 변하고 자유도가 커질수록 정규분포에 가까워짐
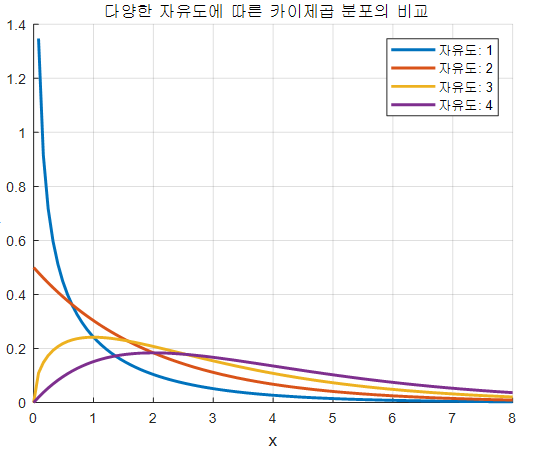
★ 모집단 분산 추론 시
F 분포(F Distribution)
:두 모집단의 분산에 대한 불편추정치의 비율
이 분산비를 활용하여 두 분산 간의 동질성 여부를 검정하거나 두 개 이상의 평균치 간의 차이 유무를 검정
★ 두 모집단 분산차이 비교시, 분산 분석, 회귀분석 등
'Data Science' 카테고리의 다른 글
| 상관분석 (0) | 2025.01.13 |
|---|---|
| 추정 (0) | 2025.01.12 |
| 확률 & 베이즈 정리 (0) | 2025.01.09 |
| 시각화 (0) | 2025.01.09 |
| 기본 용어 (0) | 2025.01.09 |



