728x90
반응형
최소 비용 신장 트리(Minimum Spanning Tree)는 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 신장트리이다.
MST를 이용하면, 도로 건설이나 전기 회로 설계, 통신 인프라 구축 등의 문제를 가장 효율적으로 처리할 수 있다.
프림 알고리즘은
시작 정점에서부터 출발해서 신장 트리 집합을 단계적으로 확장해 나가는 방법
동작 순서는 다음과 같다.
1. 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
2. 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
3. 위의 과정을 트리가 (N-1)개 의 간선을 가질 때까지 반복한다.


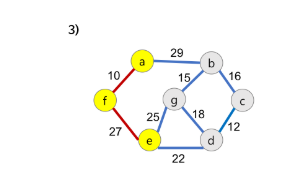



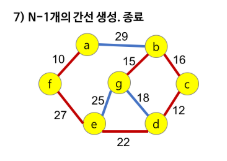
프림 알고리즘의 시간 복잡도
인접 행렬과 최소 비용값들이 들어가 있는 배열 내에서
최소 비용값을 찾는 검색을 사용할 경우, 시간 복잡도는 O(V^2)가 된다.
이진 힙 자료구조와 인접 리스트 표현을 사용한다면, O(ElogV)가 된다.
그래프에 간선이 적게 존재하는 '희소 그래프'의 경우 크루스칼 알고리즘이 적합
크루스칼은 간선을 정렬하면서 하는 간선 위주의 알고리즘
그래프에 간선이 많이 존재하는 '밀집 그래프'의 경우 프림 알고리즘이 적합
프림은 정점을 선택하면서 MST를 구성하므로 정점 위주의 알고리즘
728x90
반응형
'Algorithm' 카테고리의 다른 글
| 벨만 포드 알고리즘(The Bellman-Ford algorithm) (0) | 2019.04.28 |
|---|---|
| 퀵 정렬 (0) | 2019.04.26 |
| Union-Find(합집합 찾기) (0) | 2019.04.26 |
| 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2019.04.26 |
| 플로이드 와샬(Floyd Warshall) (0) | 2019.04.26 |


