다익스트라 알고리즘(Dijkstra 알고리즘)
다이나믹 프로그래밍을 활용한 대표적인 최단 경로 탐색 알고리즘
특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려준다.
하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다.
다익스트라 알고리즘의 경우 어떤 경우에는 다이나믹 프로그래밍, 어떤 경우에는 탐욕 알고리즘으로 분류되기도 한다.
탐욕 알고리즘이란?
현재 상황에서 여러가지 경우가 있을 경우,
그 순간의 최선의 선택을 하는 알고리즘이다.
작동 과정
- 출발 노드를 설정
- 출발 노드를 기준으로 각 노드의 최소 비용을 저장
- 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택
- 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신
- 위 과정에서 3~4번을 반복

실제로 컴퓨터 안에서 처리할 때는 이차원 배열 형태로 처리한다.
특정 행에서 열로 가는 비용을 담는 배열이다.

시작 노드를 1로 잡게 되면

1 노드에서 1부터 6 노드 까지 가는 최소 비용을 구한다.

1에서 1(자기 자신)은 갈 수 없기 때문에 0
1에서 5, 1에서 6은 연결이 되어 있지 않기 때문에 무한
현재 방문하지 않은 노드 중에서 가장 비용이 적은 노드 4번 노드를 선택한다.
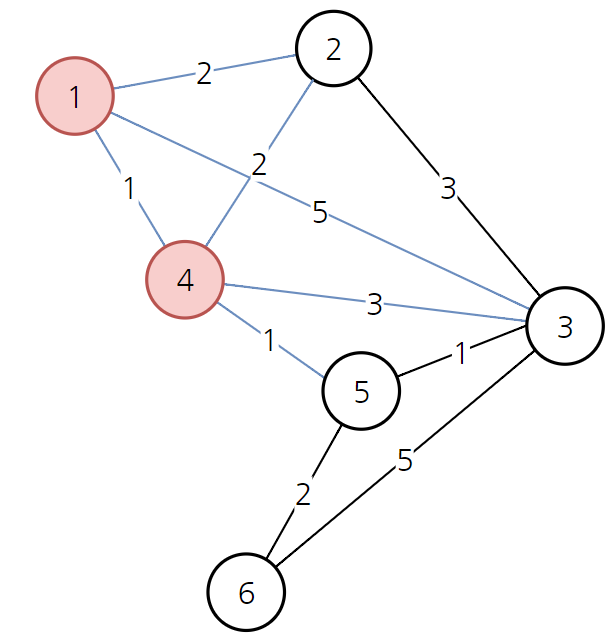
1번 노드에서 4번 노드까지 1이라는 비용이 발생한다.
그리고 앞으로 3번 노드까지 갈 수 있는 비용이 1에서 3으로 갔던 5가 있고
1에서 4로 갔다가 3으로 갈 수 있는 비용이 있기 때문에 1+3의 비용으로 갈 수 있는 경우가 생긴다.
기존의 비용보다 작기 때문에 새롭게 4로 비용을 갱신한다.

그 다음으로 방문하지 않은 노드 중에서 가장 비용이 적은 노드는 2번 노드이다.
5번 노드 또한 2의 비용으로 같지만 더 앞에 있는 노드를 선택해주도록 하겠다.

2를 거쳐 가더라도 비용이 갱신되는 경우가 없다.

다음 방문하지 않은 노드 중에서 비용이 가장 적은 노드는 5번째 노드이다.

5를 거쳐서 3으로 가는 경우 경로의 비용이 3이다.
기존의 4보다 더 저렴하기 때문에 값을 갱신한다.
5를 거쳐서 6으로도 이제 갈 수 있기 때문에 무한에서 4로 갱신한다.

방문하지 않은 노드 중에서 가장 저렴한 노드 4을 선택한다.

비용 갱신은 일어나지 않는다.

마지막 6번 노드를 선택한다.
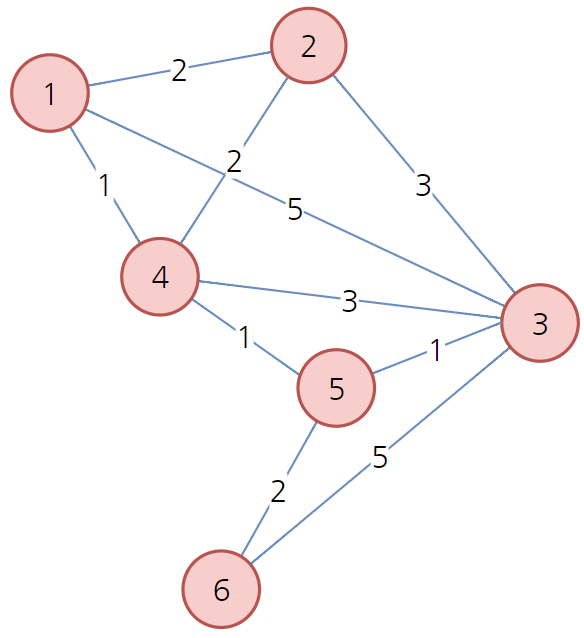
6번 노드를 방문한 후에 결과는 똑같다.
최종 배열은 다음과 같다.

선형 탐색을 써서 구현을 하면
다익스트라 시간 복잡도가 O(N^2)으로 형성된다.
따라서 최대한 빠르게 작동시켜야 하는 경우 힙 구조(priority_queue 사용)를 활용하여 시간 복잡도 O(N*logN)을 만들 수 있다.
'Algorithm' 카테고리의 다른 글
| 플로이드 와샬(Floyd Warshall) (0) | 2019.04.26 |
|---|---|
| 힙 정렬(Heap Sort) (0) | 2019.04.23 |
| 해시, 해시테이블 (0) | 2019.04.18 |
| 정렬 알고리즘 (0) | 2019.04.18 |
| 자료구조와 알고리즘 (0) | 2019.04.18 |



