728x90
반응형
Classification 개요
- Supervised learning의 일종으로, 입력 데이터에 존재하는 Feature값들과 Label값의 class 간의 관계를 학습하여 새로 관측된 데이터의 Class를 예측하는 문제
- 다음과 같은 영역에서 활용
- 이메일 spam 분류
- 고객 이탈 방지
- 어느 고객이 떠나갈 것인가? -> 떠날 위기에 있는 고객들 대상으로 고객 유치 마케팅 수행
- 이동통신회사, FedEx,체이스 은행,위키피디아 등등
- HR 직원 행동 예측
- 이직,퇴사,입사 등의 직원의 행동을 예측 -> 적절한 인력 관리에 활용
- HP,CIA,LinkedIn,국내 생명보험사 등등
- 종속변수가 수치형 -> Regression
- 종속변수가 범주형 -> Classification
- 로지스틱 회귀 변환 과정
- 승산(Odds)
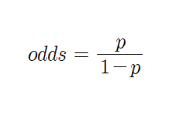
로짓함수(Logit)
-∞ ~ ∞
역함수
-0~1
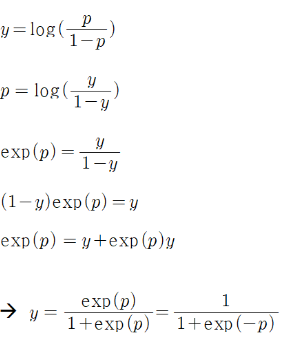
로지스틱 회귀(Logistic Regression)
- 이진 분류
- Label값으로 0/1, Y/N 등과 같이 두 가지 Class 만 가능 - 프로세스 개요
- 독립변수들의 선형 결합과 종속변수의 class 간의 확률적 관계를 학습
- gradient descent로 최적화된 Coefficients와 intercept를 계산
비용함수(Loss function)
- Maximize Likelihood / Minimize Cross-entropy
XOR 문제
- 선 하나로 분류할 수 없는 그래프(Multi layer)
임계값
- T 기본 임계값은 0.5
- P(Y=1)>=임계값이면 1로 분류
- P(Y=1)<임계값이면 0으로 분류
- 임계값을 낮추면 민감도(recall)가 높아져 오분류가 높아지더라도 Y=1인 경우를 최대한 분류
- 임계값을 높이면 Precision이 높아지게 되어 알파 오류를 최소화하는 경향이 있음
★ 임계값이 낮아지면 recall이 올라가고, 임계값을 높이면 Precision이 올라간다.
Regression과 비교
- 선형 회귀
- 종속변수는 Y값 자체
- 회귀계수는 해당 독립변수 값이 1단위 증가할 때 종속변수 Y의 변화량
- 예측오차의 최소화
- 로지스틱 회귀
- 종속변수는 Logit확률로부터 도출한 class값
- 회귀계수는 해당 독립변수 값이 1단위 증가할 때 log(odds) 변화량
- cross entropy의 초소화 혹은 log likelihood의 최대화
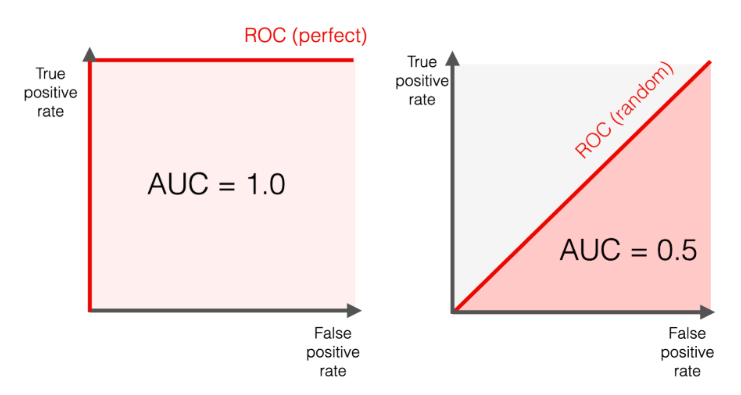
ROC(Receiver Operating Characteristic) and AUC(Area Under the Curve)
- AUC 면적이 크면 클수록 성능이 좋아진다.
728x90
반응형
'Data Science' 카테고리의 다른 글
| 선형회귀분석(Linear Regression) (0) | 2025.01.19 |
|---|---|
| 모델평가기법 (0) | 2025.01.19 |
| 머신러닝 (0) | 2025.01.18 |
| 데이터 전처리3 (0) | 2025.01.18 |
| 데이터 전처리2 (0) | 2025.01.18 |
